Quadrilateral Integration

The integral can be defined as the area between a curve (continuous and differentiable function) and the axis on some given interval.

If you want to find the area between two curves that lie on the same interval, it turns out you can subtract one from the other.  So the area in the picture here is _a∫^bF(x) - G(x) dx.
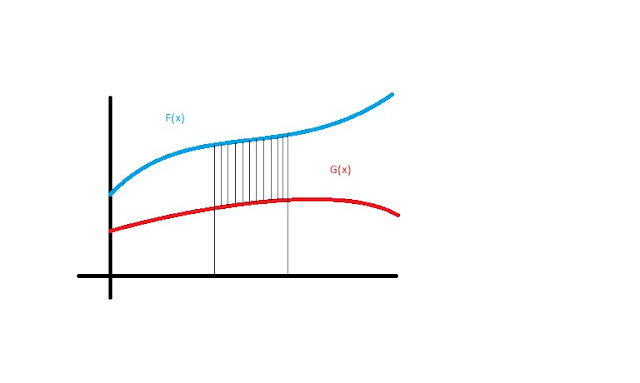
But what if the curves are on different intervals?  How can one determine a function to calculate the area?
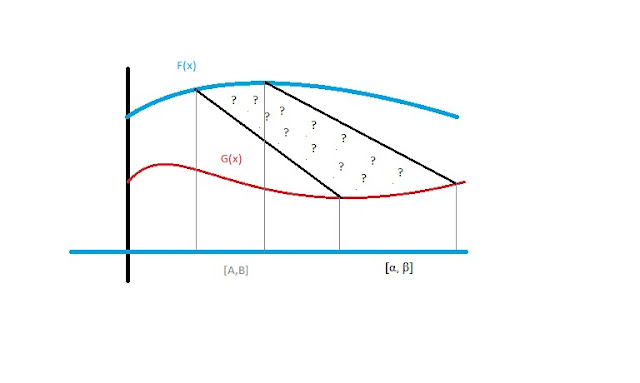A paper I wrote 2/24/2008 explores the area between curves that lie on different intervals.
It does require that for every point in the intervals on which the functions lie, the functions are able to have a line drawn between each other without intersecting.  So each point on curve F essentially must be "in view" of another point on the curve G.  The area between F (on [α,β]) and G (on [a,b]) is:

?AREA? = _α∫^βf(x)dx – _a∫^bg(x)dx + (1/2) * [(α – a)*(f(α) + g(a)) + (b – β)*(f(β) + g(b))]

I have the intervals switched in the picture, but the formula is correct for what I've typed in the line just above... (just put F on (alpha,beta), and G on (a,b) instead of what the picture shows...)

I was going to post the whole paper, proofs and all, but the formatting is weird transferring from MSWord to blog.  So I've taken screen shots of the main points of the 11 page doc.  I've cut out most of the proofs, but leave a comment if you'd like to see them. 

There is a lot of weird notation, but I tried to make it easy to follow.


*** Anything preceded by *** is extra notes outside the paper screen shots...

 *** The proof of this first theorem in mirrors the proof provided at the website: http://www.geometryalgorithms.com/ but they have deleted the original link since this paper was written.

*** Here are the terms I defined to try to explain the quadrilateral integration process.

 *** So the rest of the paper goes on to prove that the limit of this quad sum can be determined... but it does rely on this following theorem.

*** This next theorem is finding the area between a curve on one interval and another interval on the axis, and there is an example to illustrate.



 

*** Next, I find formulas to describe the lines that would form the boundary of the area between F and G.

 *** The picture for example two is a little tough to make out, but I wanted to show the lines C and D intersecting with the X axis. 

*** Theorem 5 is the main point of the paper.  This is the formula shown at the ?AREA? = part...




*** Look at this part of that formula...  (1/2) * [(α – a)*(f(α) + g(a)) + (b – β)*(f(β) + g(b))]
*** split it up...                                      (1/2)[(α – a)*(f(α) + g(a))] + (1/2)[(b – β)*(f(β) + g(b))]
*** a litle more...             (1/2)(α – a)*f(α) + 
***                                  (1/2)(α – a)*g(a) +
***                                 (1/2)(b – β)*f(β)  +
***                                 (1/2)(b – β)*g(b)
*** each of these segments is half the area of the green highlighted rectangles in this picture...

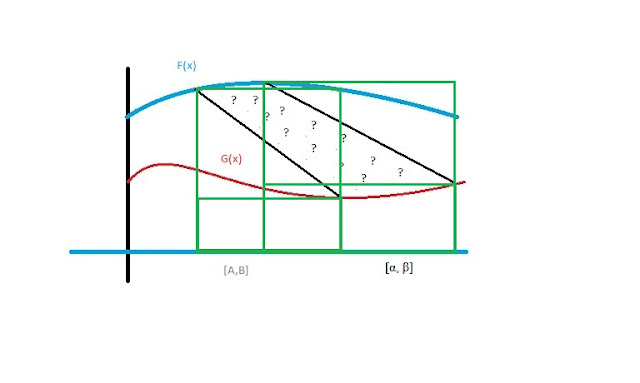
***  Using these rectangles, this would be the quick way to determine the area geometrically if the integrals of F and G were known already.  I found it pretty amazing that adding up infinitely many quadrilaterals and taking the limit gives a formula that is essentially identical to the geometrical method.

*** The following corollaries can be derived from the above theorems. 
*** There are a couple examples to illustrate what a few of the corollaries are saying.

 ***  I thought it was interesting that the quadrilateral integration can be done with regards to either axis (X or Y), so long as each F and G have inverses...

 

*** this last corollary is just to point out the connection to an existing discovery...

 *** Well that's the end of the paper....  Pretty much the whole thing now that I've gone back and looked at it, just missing the proofs (comment if you want to see them).

If you have MATLAB, below is the code I wrote to draw examples/compute values
Before you run the code, you have to input the missing values for alpha, beta, a, b; the functions F and G; and then an additional 4 values depending on which functions F and G you choose (in the second FOR loop).


The code will plot the graphs, show the partitions, and then calculate the area based on the partition size chosen.  It is the limit of this value as N reaches infinity that is the actual area between the curves.Quadrilateral Integration (DSB 2008):

alpha = %  the value desired for alpha;
beta = %  the value desired for beta;
a = %  the value desired for a;
b = %  the value desired for b;

     delta = beta - alpha;
     DELTA = b - a;
     x = 0:.1:max(b,beta)+1;

y = %  This is f(x);
y(2,:) = %  This is g(x);

plot(x,y);

n = input('partition size n = ');
     inc = delta/n;

%          this first for loop draws the partition lines%          on the plotted functions.

for i=0:n
     xfi = alpha + i*inc;
     xgi = (DELTA/delta)*(xfi - alpha) + a;
     line([xfi,xgi],[,]);
     i=i+1;
     end

area = 0; %  initialize to zero at the start

%    this second for loop calculates the area.

for i=1:n
xfi = alpha + i*inc;
xfj = alpha + (i-1)*inc;
xgi = (DELTA/delta)*(xfi - alpha) + a;
xgj = (DELTA/delta)*(xfj - alpha) + a;

x1 = xgi;
x2 = xfi;
x3 = xfj;
x4 = xgj;

y1 = % set equal to g(x1) with the actual formula...example, if G(x1) = x1, y1 = x1;
y2 = %  set equal to f(x2)   actual formula... example, if F(x2) = x2+1, y2 = x2+1;  y3 = % set equal to f(x3);
y4 = % set equal to g(x4);

A = (x1*y2-x2*y1)+(x2*y3-x3*y2)+      (x3*y4-x4*y3)+(x4*y1-x1*y4);

area = area + A/2
i=i+1;
end